747 Если записать результаты серии бросаний монеты, то может получиться, например,
последовательность:
748 Если готового датчика случайных чисел (см. предыдущую задачу) в роспоряжении программиста нет, то он может самостоятельно определить датчик в программе. Не вдаваясь в довольно сложную теорию, опишем один из таких датчиков(см.[35]). Зафиксируем некоторые натуральные a, c, m, s0 такие, что m-наибольшее из них. Определим последовательность неотрицательных целых чисел s0, s1, ... следующим правилом: sn равно остатку от деления суммы asn-1+c на m, и вместе с последовательностью s0, s1, ... рассмотрим последовательность (n = 0, 1, ...). При удачном выборе a, c,
m, s0 последовательность r0, r1, ... будет хорошо имитировать
последовательность равномерно распределенных в интервале (0, 1) случайных чисел. Одним из таких воборов
оказывается следующий:
(n = 0, 1, ...). При удачном выборе a, c,
m, s0 последовательность r0, r1, ... будет хорошо имитировать
последовательность равномерно распределенных в интервале (0, 1) случайных чисел. Одним из таких воборов
оказывается следующий:
749 Датчики случайных чисел находят интересное применение в вычислении площадей и объемов: на этом применении основан известный метод Монте-Карло (объяснение происхождения названия иподробное изложение самого метода с многочисленными примерами приложений имеется, например, в [47]). Пусть задана фигура М, целиком лежащяя внутри единичного квадрата, и пусть нужно вычислить ее площадь. Пусть в единичном квадрате выбрано наугад n точек (рис. 42) и пусть U(n) - число точек, попавших внутрь М. Тогда геометрически ясно, что при больших n площадь фигуры М будет приближенно равна U(n)/n и чем больше будет n, тем ближе мы подойдем к истинному значению площади. В качестве выбираемых "наугад" точек в этих вычислениях можно взять точки с координатами (r0, r1), (r2, r3), ..., где в роли r0, r1), ... выступают числа, получаемые с помощью датчика случайных чисел, равномерно распредеденных в интервале (0, 1).
750 Случайная числовая последовательность r0, r1, ..., члены которой равномерно распределены в интервале(0,1), может быть использована для построения случайной последовательности U0, U1, ..., члены которой принадлежат конечному множеству, состоящему из элементов x1, ...,xn. Элементы x1, ..., xn повторяются в последовательности U0, U1, ... с заданными частотами, соответственно равными p1, ..., pn (т.е. относительно последовательности U0, U1, ... можно считать, что xi встречается в ней с вероятностью pi (i = 1, ..., n), p1+...+pn=1). Последовательность U0, U1, ... будем называть случайной последовательностью с распределением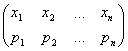 . Для построения U0, U1, ...
используется следующий прием [47]. Интервал (0, 1) разбиваем на n интервалов, длины которых равны p1,
..., pn. Координатами точек разбиения будут p1 +p2, p1 +
p2 + p 3, ..., p1 + p2 +...+pn-1. Полученные интервалы
обозначаем через I1, ..., In. Теперь перебираем числа r0, r1,
r2, ..., и если очередное число rk попадает в интервал Ij (1 ≤ j ≤ n),
то в качестве Uk берем rj(в силу равномерного распределения членов последовательности
r0, r1, ... в интервале (0, 1) вероятность попадания rk в некоторый интервал
равна длине этого интервала). Если вдруг окажется, что rk совпадает с точкой разбиения(концом интервала),
то можно условно считать, что число rk попало в интервал, лежащий справа от него.
. Для построения U0, U1, ...
используется следующий прием [47]. Интервал (0, 1) разбиваем на n интервалов, длины которых равны p1,
..., pn. Координатами точек разбиения будут p1 +p2, p1 +
p2 + p 3, ..., p1 + p2 +...+pn-1. Полученные интервалы
обозначаем через I1, ..., In. Теперь перебираем числа r0, r1,
r2, ..., и если очередное число rk попадает в интервал Ij (1 ≤ j ≤ n),
то в качестве Uk берем rj(в силу равномерного распределения членов последовательности
r0, r1, ... в интервале (0, 1) вероятность попадания rk в некоторый интервал
равна длине этого интервала). Если вдруг окажется, что rk совпадает с точкой разбиения(концом интервала),
то можно условно считать, что число rk попало в интервал, лежащий справа от него.
Предлогаются следующие задания, в которых надо воспользоваться датчиком случайных чисел:
751Для наглядной демонстрации некоторых законов теории вероятностей используется прибор, называемый доской Гальтона (рис. 44).
752 Датчики случайных чисел могут использоваться для построения на вычислительных машинах моделей сложных физических явлений. Пусть имеются два закрытых сосуда, первый из которых наполнен газом, а второй пуст. Сосуды соединены трубкой, перекрытой клапаном. После того как клапан откроют, молекулы газа будут стремиться перейти из области с более высоким давлением в область с более низким давлением. Но взаимные столкновения молекул и их столкновения со стенками сосудов и трубки будут приводить к тому, что любая из молекул может изменить свое движение на противоположное, поэтому картина выравнивания давлений в первом и втором сосудах будет непростой. В начале ХХ века физики П. и Т. Эренфесты описали интересную модель этого явления. Первый сосуд наполнен большим количеством пронумерованных шаров, а второй сосуд пуст. Третий сосуд наполнен билетиками, пронумерованными так же, как и шары. Вытягивается наудачу билетик, затем отыскивается шар с вытянутым номером и этот шар перекладывается из этого сосуда, в котором он находился, в другой сосуд. Затем билетик возвращается в третий сосуд и процедура возобнавляется. Модель П. и Т. Эренфестов очень удобно реализуется программой. Разделение n вображаемых шаров по двум сосудам может быть описано, на пример, массивом с n элементами, равными -1 (шар в первом сосуде). Вытягивание шаров легко заменить получением членов случайной последовательности с распределением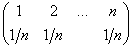 (см. задачу 750); величину n желательно брать как можно больше, не менее 1000.
Построить график или диаграмму, отмечая отношение количеств шаров в соудах через каждые 100 шагов.
(см. задачу 750); величину n желательно брать как можно больше, не менее 1000.
Построить график или диаграмму, отмечая отношение количеств шаров в соудах через каждые 100 шагов.
753 Датчики случайных чисел можно привлекать при подборе проверочных исходных данных для программ.
754 Возможно, что при решении задачи на вычислительной машине придётся вначале получать члены случайной последовательности с некоторым распределением
орел, решка, решка, орел, решка, орел, орел, орел, решка, ...
- Обозночив выпадение решки единицей, а выпадение орла - двойкой, получим
числовую последовательность
2, 1, 1, 2, 1, 2, 2, 2, 2, 1, ...
- Протокол
серии независимых испытаний, каждое из которых может иметь один из n
равновероятных исходов (в предыдущем примере n = 2), удобно изодрожать последовательностью чисел
1, 2, ..., n - номеров исходов. При n = 6 (таково,
например, число исходов при бросании игральной кости) может получиться
5, 4, 2, 1, 4, 3, 6, 6, 5, 2, 5, 6, 1, 3, ...
- Подобного рода последовательности на
практике могут быть использованы для подбора исходных данных для опытной проверки некоторой гипотезы,
многократного принятия решения в повторяющейся сложной ситуации, моделирование различных физических явлений
(например, броуновского движения) и т. д. Некоторые языки програмирования позволяют заключать в программы
обращения к так называемым датчикам случайных чисел - опреаторам или функциям, вырабатывающим при каждом
обращеннии чередовой член некоторой последовательности, похожей на рассмотренные выше. Обычно датчики
устроены так что членами последовательности оказываются целые числа r0, r1, ...,
принадлежащие интервалу (0, 1). В практических приминениях большенства таких датчиков последовательность
r0, r1, ..., может рассматриваться как последовательность равномерно распределенных
в интервале (0, 1) независимых случайных чисел, т.е. можно считать, что какой бы интервал (a, b) внутри (0, 1)
мы ни взяли, при k ≥ 0 вероятность того, что rk попадает в (a, b), не зависит от значений других
членов последовательности и равна длине b-a этого интервала. Как правило, числа r0, r1,
... при работе с датчиками образуется вовсе не случайно, а по определенному закону, лишь достаточно хорошо
иметирующему случайность, поэтому правильнее говорить о псевдослучайных числах. Однако для краткости приставку
"псевдо" часто опускают, как и упоминание о независимости чисел, и говорят о последовательности случайных чисел
или случайной последовательности, уточняя, при необходимости, характер распределения. Так будем поступать и мы.
- Предпологая провести следующие эксперименты с датчиком случайных чисел:
-
а) Получить с помощью датчика 20 чисел и оценить на глаз их "случайность" (проконтролировать отсутствие
заметны закономерностей).
б) Получить с помощью датчика 300 чисел r0, r1, ..., r299 и оценить по ним равномерность распределения: разбить интервал (0, 1) на 10 интервалов равной длины, построить столбчитую диаграмму(гистограмму) и секторную диаграмму, показывающие, сколько чисел из последовательности r1, ..., r299 попало в каждый интервал.
748 Если готового датчика случайных чисел (см. предыдущую задачу) в роспоряжении программиста нет, то он может самостоятельно определить датчик в программе. Не вдаваясь в довольно сложную теорию, опишем один из таких датчиков(см.[35]). Зафиксируем некоторые натуральные a, c, m, s0 такие, что m-наибольшее из них. Определим последовательность неотрицательных целых чисел s0, s1, ... следующим правилом: sn равно остатку от деления суммы asn-1+c на m, и вместе с последовательностью s0, s1, ... рассмотрим последовательность
 (n = 0, 1, ...). При удачном выборе a, c,
m, s0 последовательность r0, r1, ... будет хорошо имитировать
последовательность равномерно распределенных в интервале (0, 1) случайных чисел. Одним из таких воборов
оказывается следующий:
(n = 0, 1, ...). При удачном выборе a, c,
m, s0 последовательность r0, r1, ... будет хорошо имитировать
последовательность равномерно распределенных в интервале (0, 1) случайных чисел. Одним из таких воборов
оказывается следующий:
-
1) m = 2sk, где k берется настоль большим, насколько это возможно (надо иметь
в виду, что последовательность s0, s1, ..., равно как и
последовательность r0, r1, ..., будет периодической с периодом 2sk;
при небольших значениях k периодичность будет слишком заметной).
2) При делении a на 8 должен получаться остаток 5. Кроме этого, требуется, чтобы выполнялось
 .
.3) Число с должно быть нечетным; при этом желательно, чтобы выполнялось приближенное равенство

4) Число s0 можно выбрать произвольно в диапозоне от 0 до m-1.
- В связи со сказанным предпологаются следующие задания:
-
а) Подобрать несколько вариантов троек a, c, m, удовлетворяющих условию 1) - 3).
б) Найти еще какое-нибудь соображение, позволяющее хорошо имитировать случаность, и на его основе описать новый датчик.
в) Пользуясь различными датчиками, среди которых должны быть датчики, построеные по предложенной выше схеме с различным выбором a, c, m, s0, и "самодельные" датчики, построеные на других соображениях, требуется провести эксперименты, описанные в предыдущей задаче.
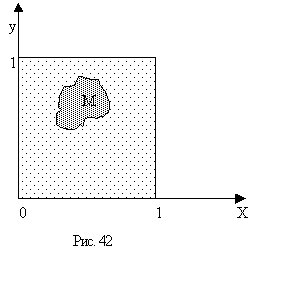
749 Датчики случайных чисел находят интересное применение в вычислении площадей и объемов: на этом применении основан известный метод Монте-Карло (объяснение происхождения названия иподробное изложение самого метода с многочисленными примерами приложений имеется, например, в [47]). Пусть задана фигура М, целиком лежащяя внутри единичного квадрата, и пусть нужно вычислить ее площадь. Пусть в единичном квадрате выбрано наугад n точек (рис. 42) и пусть U(n) - число точек, попавших внутрь М. Тогда геометрически ясно, что при больших n площадь фигуры М будет приближенно равна U(n)/n и чем больше будет n, тем ближе мы подойдем к истинному значению площади. В качестве выбираемых "наугад" точек в этих вычислениях можно взять точки с координатами (r0, r1), (r2, r3), ..., где в роли r0, r1), ... выступают числа, получаемые с помощью датчика случайных чисел, равномерно распредеденных в интервале (0, 1).
- В связи с методом Монте-Карло предлагаются
следующие задания. Воспользовавшись несколькими датчиками (в крайнем случае одним датчиком):
-
а) определить площадь круга (x - 0,5)2 + (y - 0,5)2 < 1/4; для этого найти по 200 точек с
помощью каждого из датчиков; ответ сравнить с π/4.
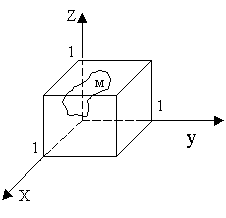
б) определить объём шара (x - 0,5)2 + (y - 0,5)2 + (z - 0,5)2 < 1/4; для этого найти по 200 точек с помощью каждого из датчиков; ответ сравнить с π/6.
750 Случайная числовая последовательность r0, r1, ..., члены которой равномерно распределены в интервале(0,1), может быть использована для построения случайной последовательности U0, U1, ..., члены которой принадлежат конечному множеству, состоящему из элементов x1, ...,xn. Элементы x1, ..., xn повторяются в последовательности U0, U1, ... с заданными частотами, соответственно равными p1, ..., pn (т.е. относительно последовательности U0, U1, ... можно считать, что xi встречается в ней с вероятностью pi (i = 1, ..., n), p1+...+pn=1). Последовательность U0, U1, ... будем называть случайной последовательностью с распределением
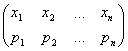 . Для построения U0, U1, ...
используется следующий прием [47]. Интервал (0, 1) разбиваем на n интервалов, длины которых равны p1,
..., pn. Координатами точек разбиения будут p1 +p2, p1 +
p2 + p 3, ..., p1 + p2 +...+pn-1. Полученные интервалы
обозначаем через I1, ..., In. Теперь перебираем числа r0, r1,
r2, ..., и если очередное число rk попадает в интервал Ij (1 ≤ j ≤ n),
то в качестве Uk берем rj(в силу равномерного распределения членов последовательности
r0, r1, ... в интервале (0, 1) вероятность попадания rk в некоторый интервал
равна длине этого интервала). Если вдруг окажется, что rk совпадает с точкой разбиения(концом интервала),
то можно условно считать, что число rk попало в интервал, лежащий справа от него.
. Для построения U0, U1, ...
используется следующий прием [47]. Интервал (0, 1) разбиваем на n интервалов, длины которых равны p1,
..., pn. Координатами точек разбиения будут p1 +p2, p1 +
p2 + p 3, ..., p1 + p2 +...+pn-1. Полученные интервалы
обозначаем через I1, ..., In. Теперь перебираем числа r0, r1,
r2, ..., и если очередное число rk попадает в интервал Ij (1 ≤ j ≤ n),
то в качестве Uk берем rj(в силу равномерного распределения членов последовательности
r0, r1, ... в интервале (0, 1) вероятность попадания rk в некоторый интервал
равна длине этого интервала). Если вдруг окажется, что rk совпадает с точкой разбиения(концом интервала),
то можно условно считать, что число rk попало в интервал, лежащий справа от него.Предлогаются следующие задания, в которых надо воспользоваться датчиком случайных чисел:
-
а) Построить 100 первых членов случайной последовательности из нулей и единиц, в которой нуль и единица
равновероятны, т.е. последовательности с распределением (
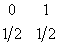 )
)б) Построить 100 первых членов случайной последовательности из цифр 1,2,3,4,5,6, в которой все эти цифры равновероятны, т.е. последовательности с распределением
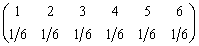 .
.в) Построить 100 первых членов случайной последовательности из нулей и единиц, в которой нуль встречается с вероятностью 1/4, а единица-с вероятностью 3/4, т.е. последоватнльности с распредилением
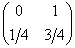 .
.г) Построить 100 первых членов случайной последовательности из слов "камень", "ножницы", "бумага", в которой эти три слова равновероятны, т.е. последовательности с распределением
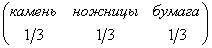 .
(Эту последовательность можно использовать для выбора ходов в известной игре "камень", "ножницы", "бумага".)
.
(Эту последовательность можно использовать для выбора ходов в известной игре "камень", "ножницы", "бумага".)д) Построить 100 первых членов случайной последовательности из слов "камень", "ножницы", "бумага", в которой слово камень встречается с вероятностью 1/3, слово "ножницы"-с вероятностью 1/2, слово "бумага"-с вероятностью 1/6, т.е. последовательности с распределением
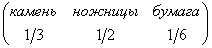 .
(Эту последовательность можно использовать для выбора ходов в известной игре "камень", "ножницы", "бумага"
со следующей системой премий: когда "камень" тупит "ножницы", присуждается одно очко, когда "ножницы" режут
"бумагу", присуждается два очка, когда "бумага" покрывает "камень", присуждается три очка.)
.
(Эту последовательность можно использовать для выбора ходов в известной игре "камень", "ножницы", "бумага"
со следующей системой премий: когда "камень" тупит "ножницы", присуждается одно очко, когда "ножницы" режут
"бумагу", присуждается два очка, когда "бумага" покрывает "камень", присуждается три очка.)
751Для наглядной демонстрации некоторых законов теории вероятностей используется прибор, называемый доской Гальтона (рис. 44).
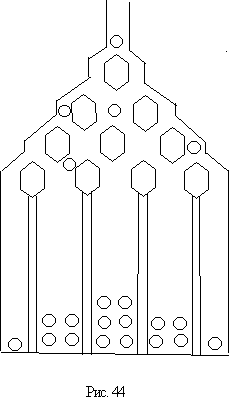
- Металлические шарики по очереди
попадают в верхний канал; встретив препятствие, они должны выбрать путь налево или направо, затем происходит
второй выбор и т. д. Каждый из выборов случаен, каждая из вероятностей выбора пути налево и направо равна 1/2.
При достаточно высоком качестве прибора наблюдаемая картина распределения шариков в нижних отделениях доски
Гальтона хорошо согласуется с вероятностными расчетами, по которым количества шариков, оказавшихся в отделениях,
пронумерованных числами 1, ..., m (на рис. 44 m=5), должны быть пропорциональными (с некоторым коэффициентом
пропорциональности, зависящим от общего числа шариков) числам из m-й строки треугольника Паскаля (см. задачу 555).
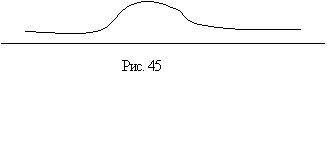
Кривая, огибающяя верхушки столбцов из шариков, должна иметь колоколообразную форму (рис. 45). Путь шарика по доске
Гальтона, содержащей m нижних отделений, можно изобразить группой из m нулей и единиц: нуль изображает выбор пути
налево, единица - направо. Получив с помощью датчика случайных чисел mn членов случайной последовательности
U0, U1, ... из нулей и единиц с распределением
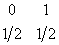 (см.
задачу 750а) и взяв группы (U0, ...,Um-1), (Um, ..., U2m-1), ...,
(U(n-1)m, ..., Unm), мы получим изображения путей n воображаемых шариков. Номер отделения,
в которое попадает шарик, определяется по количеству единиц в изображении маршрута. Пусть даны натуральные n и m
(n >= 2m). Требуется подсчитать, исходя из модели, которая основана на датчике случайных чисел,
количество воображаемых шариков, попавших в каждое из отделений. Построить графические представления результатов
подсчета (колоколообразность диаграммы или граыика будет говорить о хорошем качестве датчика.)
(см.
задачу 750а) и взяв группы (U0, ...,Um-1), (Um, ..., U2m-1), ...,
(U(n-1)m, ..., Unm), мы получим изображения путей n воображаемых шариков. Номер отделения,
в которое попадает шарик, определяется по количеству единиц в изображении маршрута. Пусть даны натуральные n и m
(n >= 2m). Требуется подсчитать, исходя из модели, которая основана на датчике случайных чисел,
количество воображаемых шариков, попавших в каждое из отделений. Построить графические представления результатов
подсчета (колоколообразность диаграммы или граыика будет говорить о хорошем качестве датчика.)752 Датчики случайных чисел могут использоваться для построения на вычислительных машинах моделей сложных физических явлений. Пусть имеются два закрытых сосуда, первый из которых наполнен газом, а второй пуст. Сосуды соединены трубкой, перекрытой клапаном. После того как клапан откроют, молекулы газа будут стремиться перейти из области с более высоким давлением в область с более низким давлением. Но взаимные столкновения молекул и их столкновения со стенками сосудов и трубки будут приводить к тому, что любая из молекул может изменить свое движение на противоположное, поэтому картина выравнивания давлений в первом и втором сосудах будет непростой. В начале ХХ века физики П. и Т. Эренфесты описали интересную модель этого явления. Первый сосуд наполнен большим количеством пронумерованных шаров, а второй сосуд пуст. Третий сосуд наполнен билетиками, пронумерованными так же, как и шары. Вытягивается наудачу билетик, затем отыскивается шар с вытянутым номером и этот шар перекладывается из этого сосуда, в котором он находился, в другой сосуд. Затем билетик возвращается в третий сосуд и процедура возобнавляется. Модель П. и Т. Эренфестов очень удобно реализуется программой. Разделение n вображаемых шаров по двум сосудам может быть описано, на пример, массивом с n элементами, равными -1 (шар в первом сосуде). Вытягивание шаров легко заменить получением членов случайной последовательности с распределением
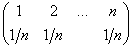 (см. задачу 750); величину n желательно брать как можно больше, не менее 1000.
Построить график или диаграмму, отмечая отношение количеств шаров в соудах через каждые 100 шагов.
(см. задачу 750); величину n желательно брать как можно больше, не менее 1000.
Построить график или диаграмму, отмечая отношение количеств шаров в соудах через каждые 100 шагов.753 Датчики случайных чисел можно привлекать при подборе проверочных исходных данных для программ.
- Получить с помощью датчика случайных чисел:
-
а) 25 действительных чисел, лежащих в диапазоне от -50 до 50;
б) 30 целых чисел, лежащих в диапазоне от -20 до 20;
в) 20 неотрицательных действительных чисел, не превосходящих 40;
г) 35 неотрицательных целых чисел, не превосходящих 100;
д) 27 натуральных чисел, не превосходящих 20;
е) натуральное n, не превосходящих 30, и n действительных чисел, лежащих в диапазоне от -100 до 100;
ж) натуральные n, m, не превосходящих 20; n целых чисел, лежащих в диапазоне от -150 до 150; m неотрицательных действительных чисел не превосходящих n;
з) 15 чисел, среди которых 7 двоек и 8 троек;
и) перестановку чисел 1, ..., 12, т. е. последовательность чисел p1, ..., p12, в которую входит каждое из чисел 1, ..., 12;
к) 28 малых латинских букв;
л) 5 неповторяющихся малых латинских букв.
754 Возможно, что при решении задачи на вычислительной машине придётся вначале получать члены случайной последовательности с некоторым распределением
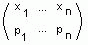
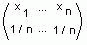
- Далее можно
придерживаться следующей стратегии. Если на вопрос pi, который предлагается самым
первым, был получен правильный ответ (правильность устанавливается сравнением полученного ответа с известным
ответом), то этот вопрос исключается из набора вопросов и происходит переход к распределению
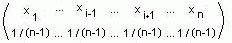
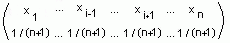
 Предыдущая глава
Предыдущая глава